Versandkostenfrei ab 75 € Warenwert**
Magnetische Flussdichte
Die magnetische Flussdichte bezeichnet laut Definition die Dichte der Feldlinien. Als sogenanntes B-Feld handelt es sich indirekt um ein Maß zur Indizierung der Stärke eines Magnetfeldes. Die Bezeichnung B-Feld ist dabei gewollt: Es handelt sich nämlich nicht um das eigentliche Magnetfeld, auch wenn die beiden Begriffe in der Literatur manchmal synonym verwendet werden.
Magnetische Flussdichte berechnen
Während laut Definition die magnetische Flussdichte durch den Buchstaben B beschrieben wird, ist der Buchstabe für das Magnetfeld das H. Es gilt mit den sogenannten Permeabilitätskonstanten μ0 (für Vakuum) und μ (für zusätzliche Materialien) der folgende Zusammenhang:
Je nach Art des Materials kann die Permeabilitätskonstante variieren:
- Solange es sich nicht um ferromagnetisches Material handelt, ist die materialspezifische Permeabilitätskonstante μ etwa 1.
- Bei ferromagnetischen Materialien kann dieser Wert auch mal bis zu 100.000 gehen.
- Wenn es sich wiederum um einen Supraleiter handelt, gilt μ = 0.
Hintergrundinformationen
Viele können alleine mit der oben genannten Formel der magnetischen Flussdichte noch nicht wirklich etwas anfangen. Die anschauliche Erläuterung der physikalischen Hintergründe sollte etwas Abhilfe schaffen: Um einen Leiter, der von Strom durchflossen wird, bildet sich ein sogenanntes magnetisches Feld. Dieses würde Kräfte auf Kobalt, Nickel, Eisen oder andere ferromagnetische Stoffe in der Nähe ausüben. Die magnetische Flussdichte B wiederum gibt an, wie stark dieses Magnetfeld tatsächlich ist. Mitunter wird sie auch als magnetische Induktion bezeichnet. B beschreibt die Dichte des magnetischen Flusses durch eine Fläche. Um diese Berechnung durchzuführen, existieren zahlreiche Formeln.
Magnetische Flussdichte vs. magnetischer Fluss – Gibt es hier einen Unterschied?
Die magnetische Flussdichte, welche durch eine gedachte Fläche läuft, ist also der magnetische Fluss. Es ist hilfreich, sich dabei ein Bild mit den magnetischen Feldlinien zwischen zwei Polen vorzustellen. Die Dichte der Feldlinien in einem Querschnitt ist quasi die magnetische Flussdichte.
Laut den sogenannten Maxwell-Gleichungen – einem sehr bekannten physikalischen Gesetz in der Elektrodynamik – können Feldlinien nicht einfach so aufhören. Die Flussdichte eines Magneten läuft deshalb in dessen Außenraum weiter. Der magnetische Fluss selbst hat das Formelzeichen Φ und bezeichnet im Grunde die Gesamtheit sämtlicher magnetischer Feldlinien. Der magnetische Fluss ergibt sich demnach durch eine bestimmte Fläche A zum Produkt mit der magnetischen Flussdichte B. Die Fläche muss senkrecht zum Fluss stehen.
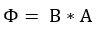Bewegte Ladungen – also Ströme – verursachen einen magnetischen Fluss. Dieser hat keinen Anfang und kein Ende, da durch Ströme ausschließlich geschlossene Feldlinien entstehen. Physikalisch korrekt bedeutet dies, dass es keine Quellen und keine Senken des magnetischen Flusses bzw. der magnetischen Flussdichte gibt. Dieses Faktum ist der Grund dafür, dass immer zwei Pole einen Magneten bilden: Ein Südpol und ein Nordpol.
Die Maxwell-Gleichungen aus der Elektrodynamik drücken diesen Sachverhalt mathematisch aus. Es ist wichtig, zu verstehen, dass bezüglich der magnetischen Flussdichte auch Permanentmagneten auf diesem Verhalten beruhen: So bilden sich dort mikroskopische Kreisströme mit einem Strom I, verursacht durch Bewegungen der Elektronen im Material. Sie sind für den magnetischen Fluss bzw. das Magnetfeld verantwortlich. Durch den Kreisstrom entsteht ein sogenanntes magnetisches Moment mit dem Südpol unterhalb der Leiterschleife und dem Nordpol oberhalb dieser Leiterschleife. Würde die Richtung des Stroms umgedreht werden, so würden die Pole vertauscht.
Physikalisch gesehen wird der magnetische Fluss deshalb über die induktive Wirkung definiert, die er auf eine Leiterschleife ausübt. Wenn eine Leiterschleife mit einer bekannten Fläche in ein Magnetfeld gebracht wird, indiziert dieses dort einen Spannungsstoß. Der magnetische Fluss ist gleich dem zeitlichen integral über diesem Spannungsstoß:
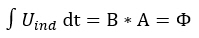Der magnetische Fluss wird mit dieser Leiterschleife und der darin induzierten Spannung gemessen. Dies jedoch ist keine gängige Methode mehr: Eine sogenannte Hall-Sonde ist viel genauer. Verläuft die magnetische Flussdichte durch eine gekrümmte Fläche, ist der magnetische Fluss als Integral über der Flächennormalen der vektoriellen Flussdichte zu definieren:
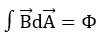Feldlinien, die durch eine geschlossene Oberfläche hineintreten – beispielsweise die Oberfläche einer Kugel – , müssen dort auch wieder heraus. Dies ist die Natur geschlossener Feldlinien: Mathematisch wird das darin manifestiert, dass der magnetische Fluss durch geschlossene Flächen stets Null ist. Es existieren demnach keine Quellen oder Senken bei der magnetischen Flussdichte.
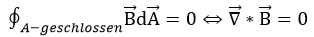Äquivalent dazu ist die Aussage einer der vier Maxwell-Gleichungen über die sogenannte Divergenz Freiheit der magnetischen Flussdichte.